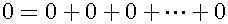Pi is a mysterious number, which has attracted many mathematicians and many math lovers. However, the exact value of it is still unknown. Until now, many strange features of it were elucidated. Especially, Lindemann proved that pi is a transcendental number. That is, it isn’t an algebraic number. Although Lindemann’s proof is difficult to understand, I represent a very easy proof here. In the beginning, definitions 1 to 3 of Elementsare shown below.
Definition 1: A point is that which has no part.
Definition 2: A line is the breadthless length.
Definition 3: The ends of a line are points.
The shortest distance between two points is the length of the straight line between them. That is, the length means that of the straight line. If we thought naturally, because a line is the breadthless length, it must consist of straight lines. However, a circle contains no straight line. As the logical consequence, it cannot exist. Nevertheless, Euclid defined a circle by force. His definition of it is as follows.
Definition 15: A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure equal one another.
Definition 16: And the point is called the center of the circle.
Definition 17: A diameter of the circle is any straight line drawn through the center and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
Firstly, he assumed the existence of a line, which corresponds to a circumference of a circle. Secondary, he determined the location of points on it. Eventually, he assumed the existence of a circle. Still, he couldn’t define the length of the circumference.
The lack of the definition of the length of the circumference causes many paradoxes. The famous one is Aristotle’s wheel paradox. Figure 1 shows it.
A wheel consists of two concentric circles of different diameters. They are rigidly connected. If the large circle makes one complete rotation along the line segment BB, the small circle also makes one complete rotation along the line segment CC, and simultaneously, the center point A moves along the line segment AA. These three lines have the same length. That is, There is a one-to-one correspondence between points on the large circle and points on the small circle. So, circumferences of them seem to be equal. This is a paradox.
Galileo considered this paradox deeply, and then he wrote his thought experiment in Dialogue Concerning Two New Sciences. Figure 2 shows the simplified thought experiment. In the beginning, consider two rigidly connected concentric squares: the square ABCD is large, and the square EFGH is small. Next, the square ABCD is rotated around the point D until the side CD coincides with the line AP. Simultaneously, square EFGH is rotated until the side HG coincides with the line EQ. Next, the square ABCD is rotated around the point C and so on. Finally, these two squares make a complete revolution. Then, the large square has imprinted four lines on the line AP without a break. In contrast, the small square has imprinted four lines equal to its perimeter, but they are separated by four intervals.
 |
| Figure 2 |
This exposition is applicable to all other polygons. Galileo says as follows.
Let a large polygon of, say, one thousand sides make one complete rotation and thus lay off a line equal to its perimeter; at the same time the small one will pass over an approximately equal distance, made up of a thousand small portions, each equal to one of its sides, but interrupted by a thousand spaces which, in contrast with the portions that coincide with the sides of the polygon, we may call empty. So far the matter is free from difficulty or doubt.
Therefore, when considering the length of the circumference, it will be better to approximate a circle by a regular polygon. This is the natural conclusion because Euclid defined the length as the length of the straight line.
Furthermore, a line segment of any length contains the same number of points. This fact is shown in Figure 3-1. There are the longer line A1A2 and the shorter line B1B2. They are parallel. The line A1B1 crosses the line A2B2 at the point O. Consider an arbitrary point An on the line A1A2. If we draw a line from the point An to the point O, the line AnO crosses the line B1B2 at the point Bn. That is, every point on the line A1A2 corresponds to a point on the line B1B2.
Let us take a step further. We shall focus on the point O. It is the end of five lines in figure 3-1. If they are separated at the point O, five ends of lines are generated. Figure 3-2 shows separated five lines. There are the point An, the point Bn and the point On on the line AnOn. The number of them is the same as the number of lines. This is natural. Because Euclid defined that the ends of a line are points, the number of points necessarily corresponds to the number of lines. So, the point An and the point On are ends of the line AnOn, and the point Bn is the intersection point between the line B1B2 and AnOn. That is, a point is generated as an end of a line. Consequently, it is not a substantial entity. It is divisible without limit.
After all, the length of the circumference cannot be defined. We can only estimate it. Archimedes was the first mathematician to estimate scientifically the value of pi. He estimated it by the perimeter of the regular polygon in Measurement of a Circle. The length of the circumference is between the perimeter of the inscribed regular polygon and the perimeter of the circumscribed regular polygon. Firstly, he used the hexagon. Subsequently, he duplicated the number of sides. Figure 4 shows the approximation by the hexagon and the dodecagon. Finally, he used the 96-gon.
 |
| Figure 4 |
ここに記述してください。